#4 測定値の変化の大きさに意味があると言うためには

１．経験的方法
　蓄積されたこれまでの測定値の傾向や、コーチの観察とデータの照らし合わせ等による実際のパフォーマンス上の差から経験則に基づいて判断する方法です。　例えば筆者の経験で、大学生のサッカー選手において、20mスプリントで2.97～3.15秒の範囲にある選手集団では、0.02秒の差であれば計算上約13cmの差しかありませんが、0.03秒の差があれば約20cmの差、0.04秒の差では約25cm、そして0.05秒の差がつくと約30cmの差となり、この差が付くと、速い選手は自分の肩を相手の前に確実に割り込ませることができる差ということが言えます。　このことから、20mスプリントテストの結果、0.05秒以上短縮できれば、大学生サッカー選手にとって意味のある変化であると判断することができます。そして0.05秒未満の変化では意味のある変化であるとは見做さないことになります。こうした経験的方法は、他の競技においてもジャンプにおける地上高や、反応を含めたスタートダッシュやアジリティーにおいても用いることができます。

２．測定の標準誤差（TE）による方法
　必然的に測定値に含まれている誤差は、測定の標準誤差（Standard errorof measurement）、または常に普通に起こりうる誤差という意味のTypicalErrorの頭文字を取ってTEと呼ばれています。2回の測定、例えばトレーニング前とトレーニング後に測定を実施した際に、個人に示された差がこのTEよりも大きければ意味のある差である、と考えることができます。

　TEの計算法それ自体は非常に簡単で、例えばあるグループのトレーニング前とトレーニング後といった2回の測定値があるとすると、TE＝個人ごとの2回の測定値の差のグループ全体における標準偏差（SD）÷√2で得られます。なぜこの公式でTEが求められるかという統計学的根拠は複雑ですが、簡単に言うと、2回のテストそれぞれに含まれるTEの分散は2回のテストの測定値間の差が合わさったものであると考え、分散がSDの2乗であることに由来します。

　TEの計算法はこれ以外に、TE×1.96あるいはTE×2とする方法や、TE×1.96×√2とする方法もありますが、数値が高くなるため競技レベルが高くなると現実的にその値を超えることが困難となるため、競技レベルを考慮してどれを使用するかを判断する必要があります。　

　表1の具体例を基に説明します。

　20名の選手それぞれの10mスプリントタイムのトレーニング前とトレーニング後の差が示されています。差の平均値は、-0.02でその標準偏差は0.031でした。これを基にTEをエクセルで計算するとTE＝SD/SQRT（2）ですから、その値は0.022となります。0.022以上タイムを短縮した選手については、実質的な差があったと見做すことができます。これをクリアしているのは、H、M、N、O、P、Rの6名のみとなり後は誤差範囲であると判断することになります。TE×1.96で計算すると0.043となり、実質的なタイム短縮をしたと言えるのは、OとPの2名のみとなります。その他の方法ではさらにTEを超えることが難しくなります。　

このような厳密な判断を行うためには100分の1秒が正確に測定できる光電管（例えばWitty）やレーザーを用いたタイム計測機器（例えばDashr）が不可欠であり、目視による手動計測では誤差が大きすぎて意味をなさないことは言うまでもありません。

3． グループの標準偏差を用いて目標値を設定する方法
　以上は2回の測定値間の差についてその標準誤差を用いた判断でしたが、1回の測定値を測定した集団における標準偏差から判断する方法もあります。

　この計算方法もとてもシンプルで、グループのデータから得られたSD×0.2で計算します。SDの0.2倍をもって意味のある差であると判断できる理由は、効果量Cohenのdにおいて差があると認められる最小の値である0.2に対応しています。

　別の例で見てみましょう。表2の記録の列には、スタートから20mと30m地点に設置した光電管の通過タイムで距離10mを割って時速（km/h）に直したスピードを示しています。わかりやすいように降順で配列しています。

　この標準偏差は0.98ですからこれに0.2を掛けた0.197を上回れば、実質的な向上であると判断できます。　次のテストで0.197km/hを上回るかどうかをチェックしてもいいのですが、ここではこの値を各選手の記録にプラスすることで目標値を設定してみましょう。その値が目標値の列の数字です。次のテストでこの値を超えることができれば実質的な向上とみなせると判断できるわけです。

　このように、最小有効変化量は、得られた変化に意味があるかどうかという判断に用いるだけではなく、それを基に目標設定をすることも可能なのです。
 

4．変動係数（CV）を用いる方法
　個人のデータが定期的に高い頻度で、信頼性のある方法で取得されている場合に生じた変化量に意味あるかどうか、という判断をする際に用いられる方法に、変動係数（CV）注）を用いる手法があります。それまでに取得されたすべてのデータから得られる変動係数に0.3を掛け(0.3CV)、その上限と下限の値を超えたときに、実質的な向上が見られた、あるいは明らかに体調を崩しているといった判断するという方法です。

注）変動係数とは標準偏差を平均値で割って標準化した値で、単位や平均値の大きさにかかわらない相対的なばらつきを表す統計量。通常100を掛けてパーセントで表す。Coefficient ofVariationの略でCVと記されることが多い。

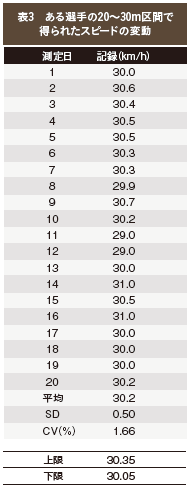
　表3は、ある選手の静止状態からのスプリントにおける20～30m区間で得られたスピードを20日間にわたってほぼ毎日３～5回測定し日々の最高値を並べたものです。
 

　0.3CVによって上限と下限を求めるには、パーセントで表されている変動係数をまず100で割って少数に直し、それに0.3を掛け、その値を平均値にかけて変動量を出し、それを平均値にプラスまたはマイナスして上限と下限を求めます。エクセルでは、＝平均値±平均値*(変動係数/100)*0.3で求めることができます。

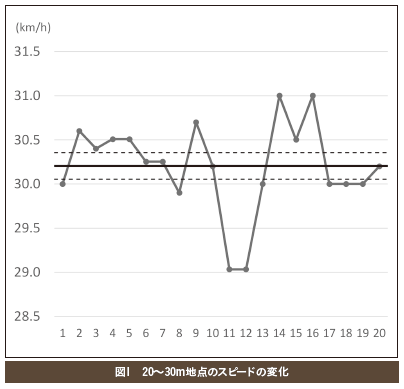
　以上の結果をグラフ化したものが図１です。縦軸に時速、横軸が測定日です。中央の太い実線がこの間の平均値、上下の破線が限界値を示しています。11日目と12日目に大きく体調を崩していることがうかがえます。そして14日目と16日目にベスト記録が出ています。　

　この結果から、次回以降のテストで上限を30.35km/h上回る記録が確実に安定して出せるようになれば間違いなくスピードが向上してきていると判断することができます。
 

データは収集することに価値があるのではなく、そこから様々な判断や意志決定をするためのもの。

 

まとめ
　以上のように、SWCにはいくつかの方法があります。どれを採用するかは、競技レベルや目的によって適宜使い分ける必要があります。

　今日、トレーニング指導の様々な場面で、誰にでも手軽に妥当性と信頼性のある客観的なデータが収集できるようになっています。データは収集することに価値があるのではなく、そこから様々な判断や意志決定をするためのものです。単に数値が大きくなった小さくなったというだけに左右されることなく、判断や意志決定における合理性を高めるためには、得られたデータに対して今回紹介たような統計的な処理を施すことが求められます。
　ぜひ皆さんも手元のデータをもとに今回紹介した手法を適用して、その結果からどんなことが言えるか試してみてください。